Skip to main content

Introduction to NV Centers, Electron Spin, and ODMR

1. What is an NV Center?​

An NV center (“Nitrogen-Vacancy”) is a point defect in the crystal lattice of diamond, consisting of:

  • a nitrogen atom replacing a carbon atom, and
  • an adjacent vacancy.

In its negatively charged form (NV⁻) it contains 6 electrons, distributed over four molecular orbitals ($a_1$, $a_1'$, $e_x$, $e_y$). Two electrons with parallel-aligned spin occupy the degenerate orbitals $e_x$ and $e_y$, resulting in a total spin S = 1.

2. What is Spin?​

Spin is a fundamental quantum-mechanical property of particles, analogous to an intrinsic angular momentum. It is:

  • not a real rotation, but a quantized property with two possible states for the electron:

    ms=+12(spin-up),ms=−12(spin-down)m_s = +\tfrac{1}{2} \quad \text{(spin-up)}, \quad m_s = -\tfrac{1}{2} \quad \text{(spin-down)}

  • responsible for:

    • the Pauli principle: no two electrons can occupy the same quantum state.
    • Hund’s rule: orbitals are singly filled with parallel spins first.

In NV centers the spin value is even $S = 1$, allowing three projections: $m_s = 0, +1, -1$.

3. Energy Levels in the NV Center​

The NV center has:

  • a triplet ground state $|g⟩$,
  • a triplet excited state $|e⟩$,
  • a non-fluorescent singlet intermediate state $|s⟩$.

Through spin-spin interactions (even without a magnetic field!), the ground state is split into:

  • $|g, m_s = 0⟩$ and
  • $|g, m_s = ±1⟩$

The energy splitting is:

Dg≈2.87 GHzD_g \approx 2.87 \text{ GHz}

4. Optically Detected Magnetic Resonance (ODMR)​

Basic Idea​

  • The NV center is excited with green light (532 nm).
  • It fluoresces in the red range (~637–800 nm) depending on the spin state.

Fluorescence Pathways​

  • $|e,0⟩ \rightarrow |g,0⟩$: radiative transition → bright fluorescence
  • $|e,±1⟩ \rightarrow |s⟩ \rightarrow |g,0⟩$: non-radiative → dark

Microwave Excitation​

  • Microwaves at 2.87 GHz induce spin flips between $|g,0⟩$ and $|g,±1⟩$.
  • The electron ends up in a less fluorescent state ⇒ dip in fluorescence.

With External Magnetic Field​

  • A static magnetic field along the NV axis causes a Zeeman effect, further splitting $|g,+1⟩$ and $|g,-1⟩$.
  • Two resonance frequencies appear ⇒ two dips in the ODMR spectrum.

5. Key Questions and Answers​

▶ Why do the $m_s = ±1$ states split?​

Due to zero-field splitting from spin-spin interaction in the crystal field.

▶ What is the singlet state?​

A non-radiative intermediate state through which electrons from $|e,±1⟩$ relax to $|g,0⟩$ – without photon emission.

▶ How does the electron go from $|g,0⟩$ to $|g,±1⟩$?​

Via targeted microwave excitation at 2.87 GHz, matching the energy splitting.

6. ODMR Signal – What Is Measured?​

  • The ODMR signal is the fluorescence intensity as a function of microwave frequency.
  • Without microwaves: maximum fluorescence.
  • At resonance: fluorescence decreases (spin is flipped out of $m_s = 0$).
  • With magnetic fields: two absorption dips instead of one.

7. Why Is This Important?​

  • Quantum sensing: precise measurement of magnetic fields (nanotesla range).
  • Quantum information: spin states serve as qubits.
  • Biophysics & materials science: sensors for temperature, electric fields, pH, etc.

8. Summary Mnemonic​

9. States:​

1. Optical Excitation Only (532 nm, no Magnetic Field, no Microwave)​

The NV center is excited with a 532 nm laser: electrons go from the ground state $|g⟩$ to the excited state $|e⟩$. There are two pathways back:

  • $|e,0⟩ \rightarrow |g,0⟩$ with strong fluorescence
  • $|e,±1⟩ \rightarrow$ non-radiative transition via singlet state $|s⟩ \rightarrow |g,0⟩$ ⇒ reduced fluorescence

Result: most NV centers end up in $|g,0⟩$. This is called optical pumping into the $m_s = 0$ state.

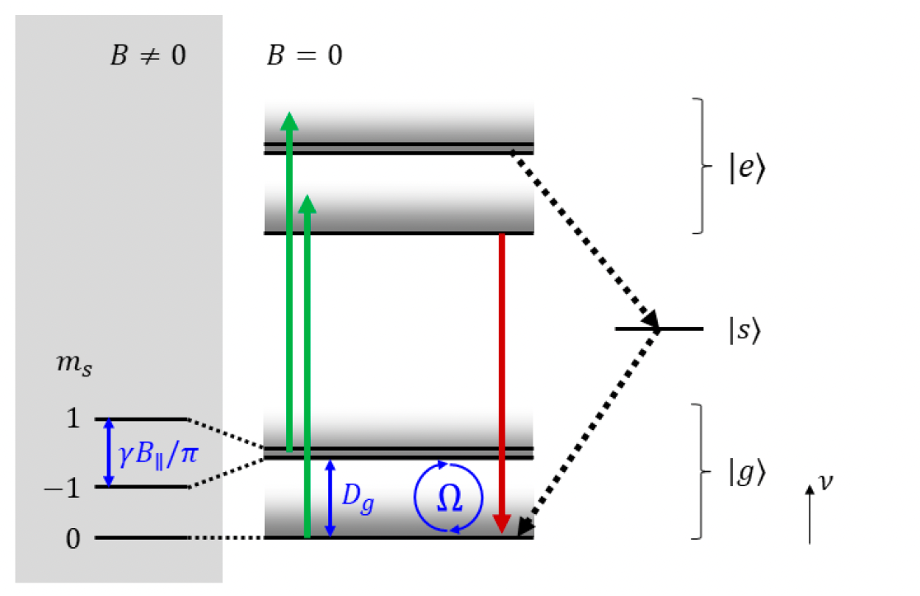
2. Optical Excitation + Microwave (2.87 GHz)​

A microwave at 2.87 GHz matches the splitting between $|g,0⟩$ and $|g,±1⟩$ (zero-field splitting $D_g$). This induces a spin flip:

  • Electrons are periodically swapped between $|g,0⟩ ⇄ |g,±1⟩$ (Rabi oscillations).

Consequence: more electrons end up in $|e,±1⟩$, which then relax via the singlet state ⇒ fluorescence darkens.

3. Optical Excitation + Microwave + External Magnetic Field​

An external magnetic field $B∥$ along the NV axis splits the degenerate $m_s = ±1$ level (Zeeman effect). Now there are two distinct resonance frequencies: $|g,0⟩→|g,+1⟩$ $|g,0⟩→|g,-1⟩$ Sweeping the microwave frequency → two dips in fluorescence. This is the typical ODMR signal under a magnetic field.