Lens

Lenses

In ray optics, light is represented as a bundle of rays (arrows), which simplifies the physical properties of light. A ray has a direction and is therefore drawn with an arrow. A lens "refracts" the beam, changing its direction.

The focal length of a lens corresponds to the distance from the lens to the focal plane on which the focal point lies. It is given in millimeters (f = mm).

Converging (positive) and diverging (negative) lenses

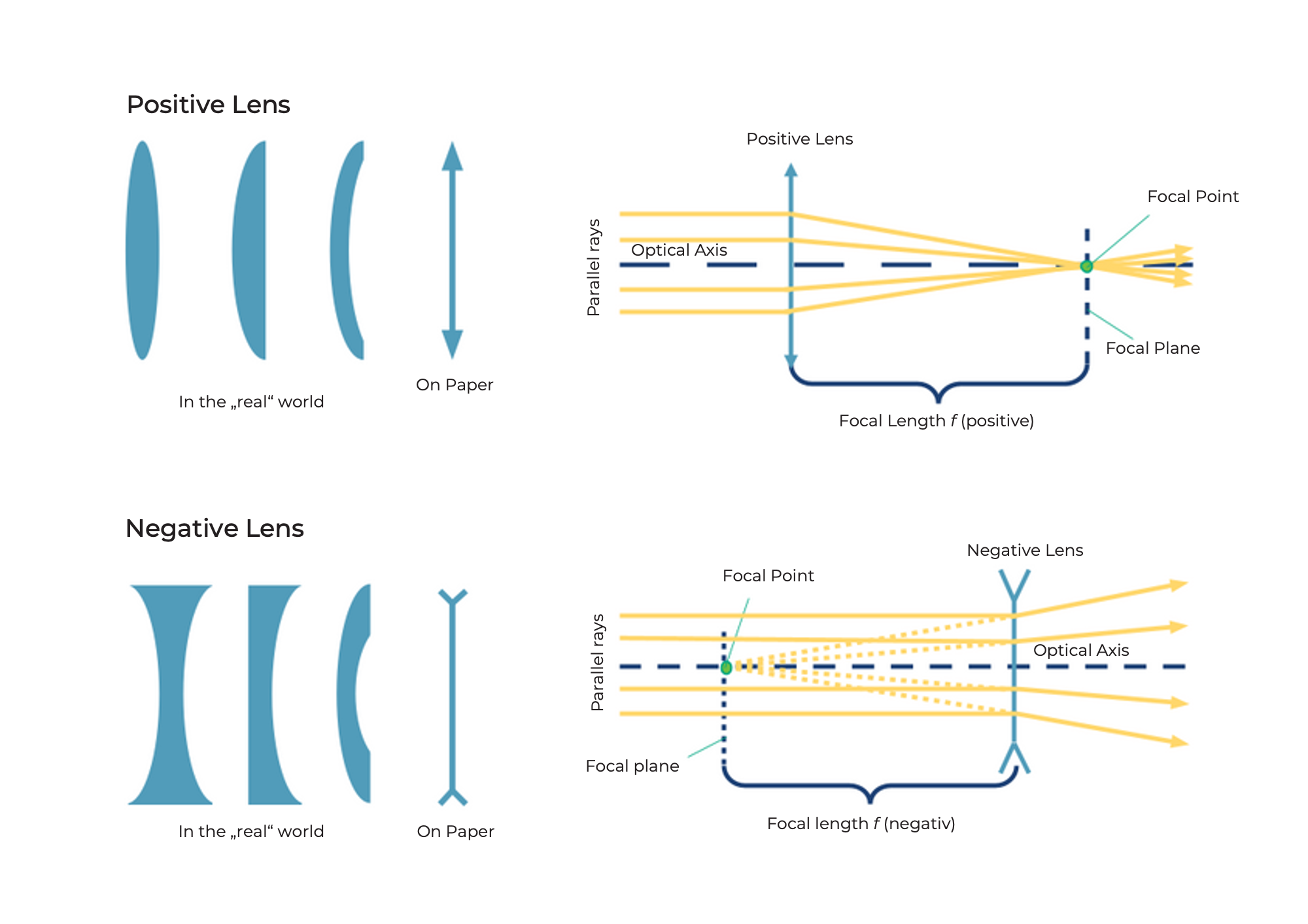
Converging lenses refract the rays of light traveling parallel to the optical axis at a point called the focal point.

The diverging lenses refract the rays of light traveling parallel to the optical axis as if they originated from a point called the "virtual" focus.

Lenses “refract” the rays of light

You can find the focal length of the lens as a printed number on the lens holder. The MiniBOX receives a 100mm converging lens, two 40mm converging lenses and a -50mm negative lens. The numbers indicate the focal length.

The converging lens is also called a positive or convex lens. The middle part of the lens is always thicker than the edge.

The converging lens enlarges the image. The magnification is different for the 40mm lens and the 100mm lens. The image can be upright or inverted.

The negative lens (spreading lens) is sometimes also called a negative or concave lens. The middle part of the lens is always thinner than the edge.

With the negative lens (here: -50 mm lens) the image is always reduced and always upright

We assume that our lenses are so-called "thin lenses". This means we can consider them as one plane and not care about their thickness. This makes explanations and calculations much easier.

Did the answers raise any more questions? Then drive to find out exactly how lenses work...

Lens image

Now take the lentil cubes. With the right lens, try to decipher the focal length information in the cubes shown. Move the lens over the writing until it is the same size as the "UC2" text.

Can you see the text the same size and orientation as the "UC2"? What happens when you change the distance between the lens and the image?

What happens if you use a lens with the wrong focal length?

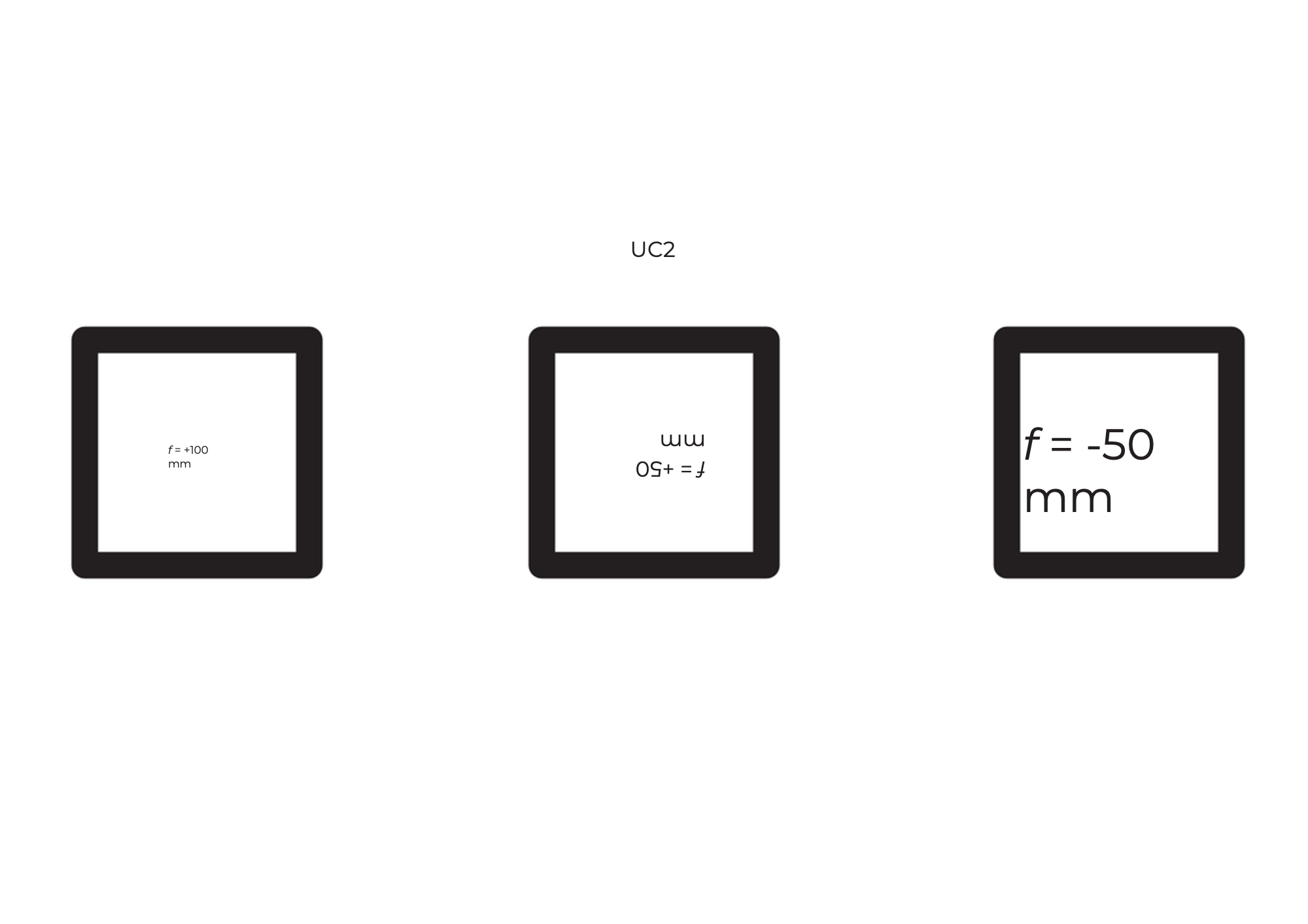
Image of an object through a positive lens

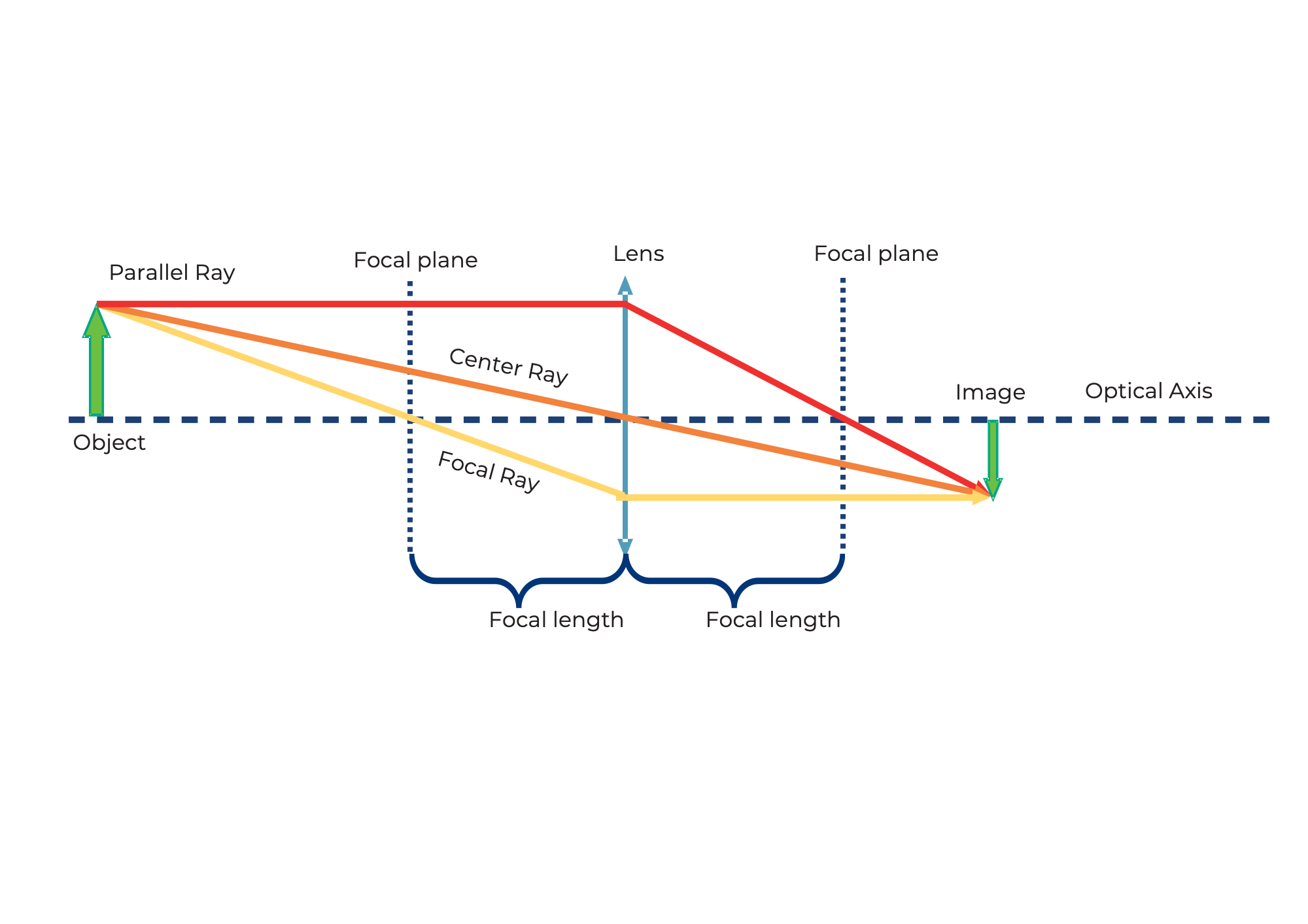
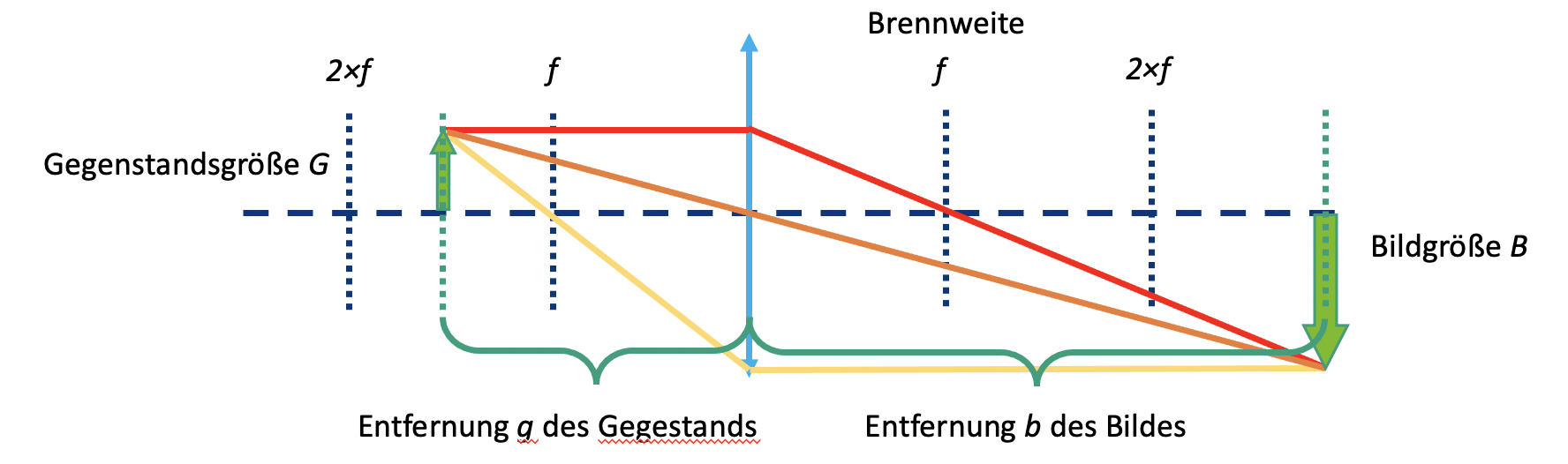
Let's take the converging lens as an example. We start with an object (green arrow) and see what happens to the rays that start from the top. There are infinitely many rays in all directions, but for drawing the figure the following three rays will suffice:

1. The centre beam (orange) passes undisturbed through the center of the lens.
2. The focus ray (yellow) also starts from the tip of the arrow, but goes through the object-side focus at focal length f. After the lens, it continues at the same height, but now parallel to the optical axis.
3. The parallel beam (red) initially runs parallel to the optical axis, but is then refracted at the lens in such a way that it passes through the focal point on the image side at focal length f.

The image is formed where all the rays intersect. The principle is used for all points or the rays of an object emanating from them. Depending on which lens is used and depending on the position of the object, the properties of the image change, such as size, orientation and position.

Image of an object through a negative lens

In the case of the negative lens, we use the same method to image the ray path. Unlike the case of the converging lens, the image is always reduced and virtual. Magnification depends on the position of the object in front of the lens. Unlike the converging lens, the image is created on the object side and is therefore called a virtual image. You can see it directly with your eyes but not project it onto a screen.

The way a lens creates an image is predictable by knowing the focal length of that lens. Therefore, a certain distance must be maintained so that you can see the writing with the specified lens on the previous sheet.

The magnification and the location where the image is formed depend on the focal length of the lens and the distance between the lens and the object.

With the diverging lens (f = -50 mm) you always see a reduced virtual image. A virtual image can only be viewed with the eye. So far we only have virtual ones seen pictures.

The converging lens as a magnifying glass

Take the UC2 lens cube with focal length f=40mm and use it as a magnifying glass.

Can you read the small letters through the converging lens? What is written there?

A lens in action can be found here:

That's what converging lenses do

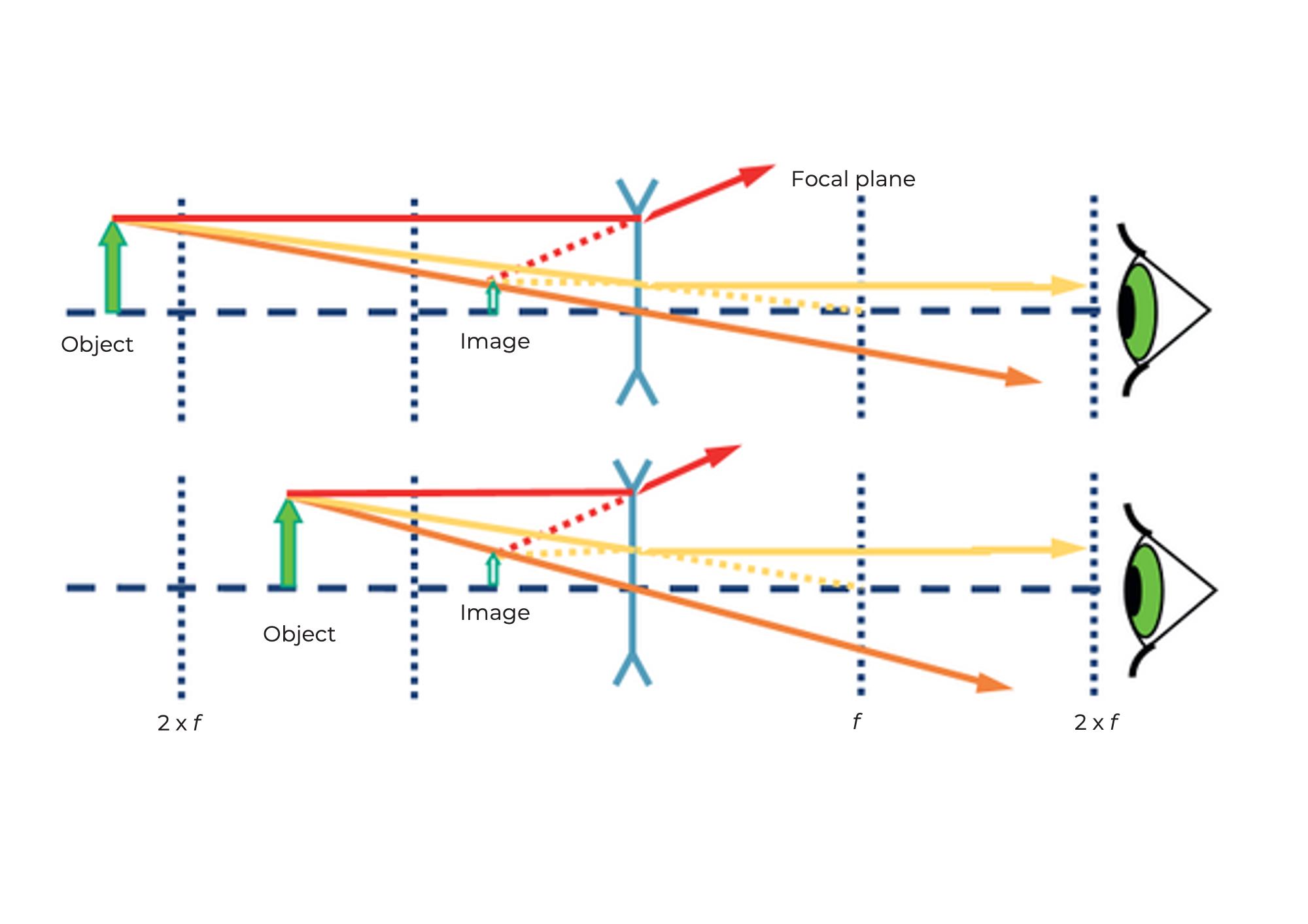
With the converging lenses, the image and the magnification depend on the position of the object.

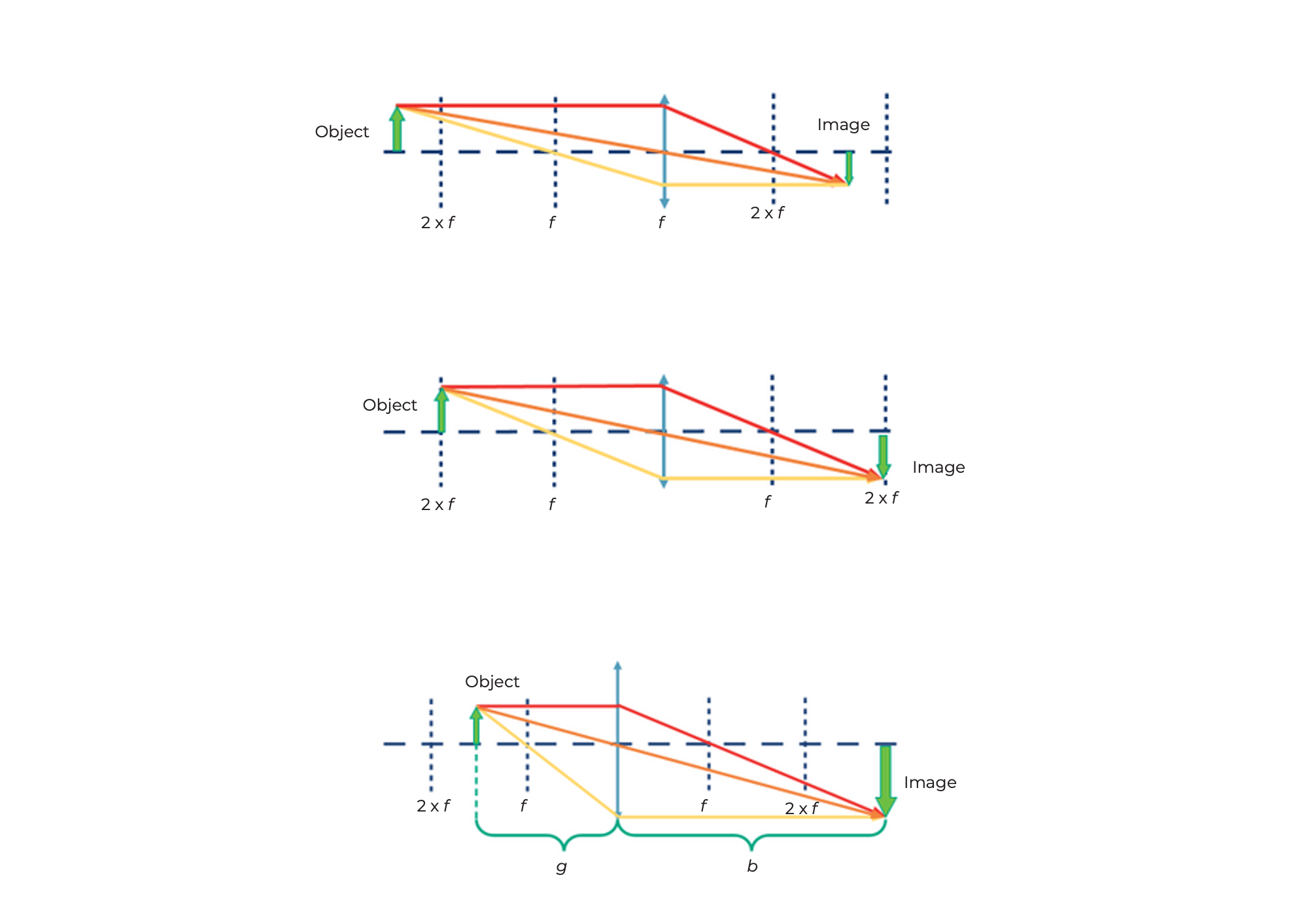
If the distance between the object and the lens is more than twice the focal length of the lens, then the image is...

• Vice versa
• Swapped sides
• Reduced
• Real

If the distance between the object and the lens is exactly twice the focal length of the lens, then the image is...

• Vice versa
• Swapped sides
• Same size
• Real

If the distance between the object and the lens is more than the focal length and less than twice the focal length of the lens, then the image is...

• Vice versa
• Swapped sides
• Magnified
• real

Object distance (g)

The distance between the object and the lens plane is called g.

Image width (b)

The distance between the lens plane and the image formed by the lens is denoted as b.

The converging lens can produce a real image. The real image can then be seen on a screen.

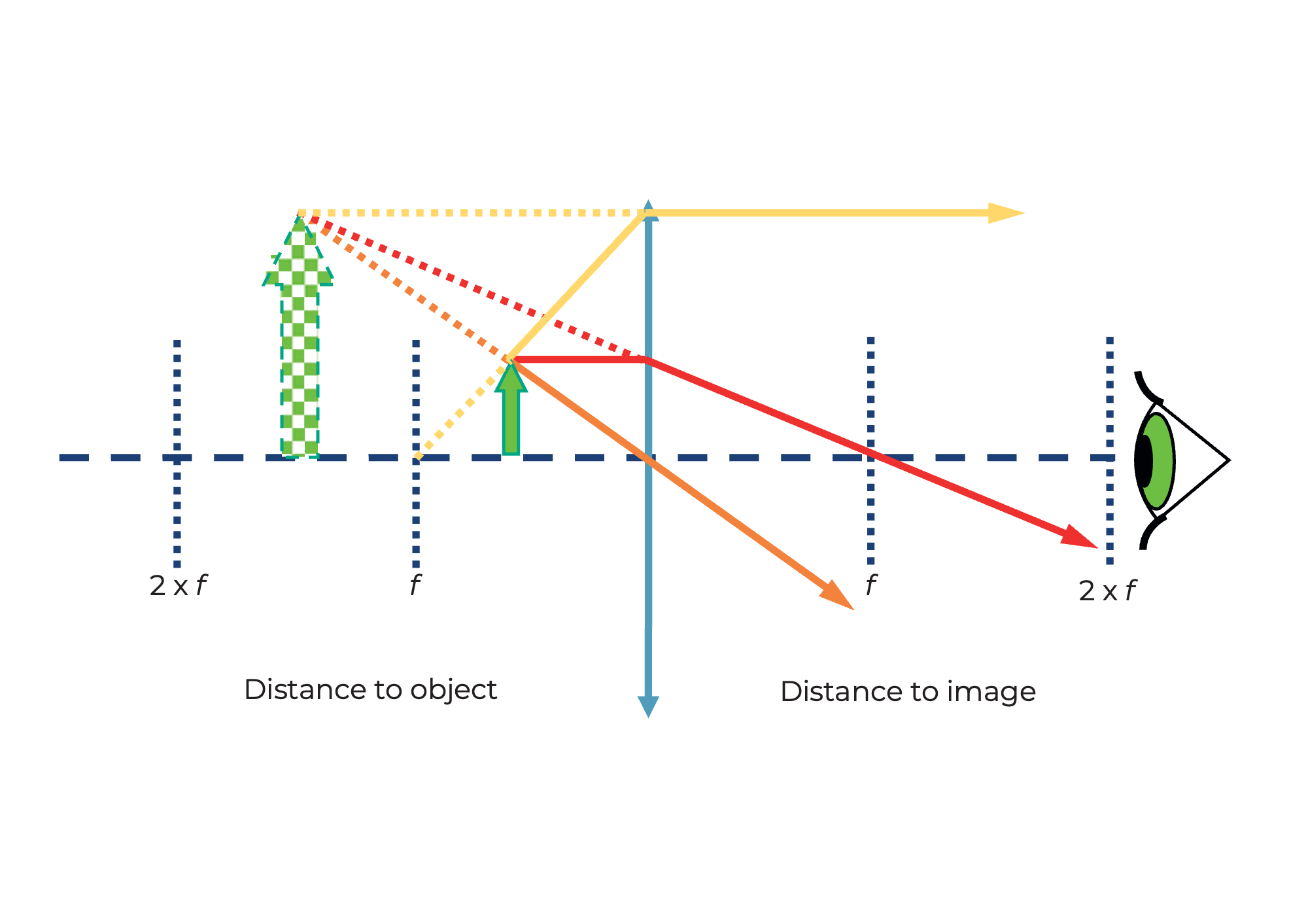
That's why the magnifying glass enlarges

Magnifying glass effect!

If the distance between the object and the lens is less than the focal length of the lens, then the image is...

• upright
• right side up
• Magnified
• Virtual

The magnifying glass is the simplest of all optical devices, since it consists only of a simple converging lens with a suitable focal length. Why does the cube with the 50 𝑚𝑚 enlarge the small text? If the object is in front of the focal length of the lens - i.e. less than 50 𝑚𝑚 in front of the lens - the lens creates a virtual image which is behind the actual object. The eye perceives it enlarged. Check out the diagram above.

Calculate the magnification of the magnifying glass using the following formula:

250 𝑚𝑚 is the distance of clear visual range - i.e. the distance between the object and the eye at which most people can read well. More on this later in the “accommodation” of the eye.

How does a cinema projector work?

Take the UC2 lens cube with focal length 𝑓 =40 𝑚𝑚 and place it behind the sample holder cube. The distance between the object and the lens (i.e. the object distance g) should be approx. 50 mm. If you now illuminate the object with the flashlight, you will see it sharply at a distance of approx. 200 mm on the wall. A cinema projector has a film strip instead of the object and of course a much stronger light source.

Use a flashlight (e.g. from your cell phone) as a light source and hold it in front of the object

Use the image or text on the microscope slide as the object

How is the image oriented? Slide the lens back and forth in the cube and see when the image is in focus. Find the image for g = 50mm, 60mm, 65mm and measure the distance between the lens and the image.

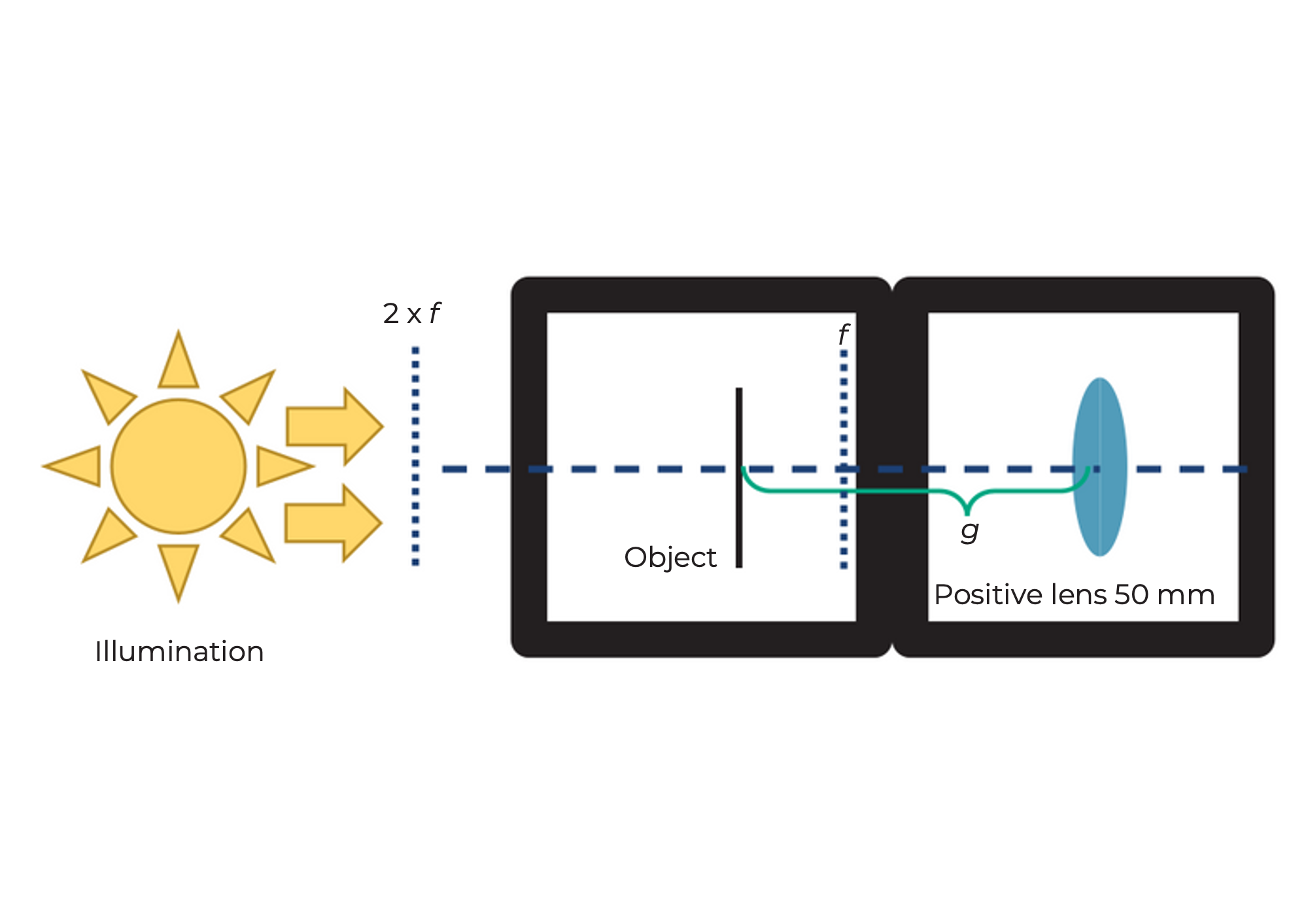
How does a cinema projector work?

Where is the picture?

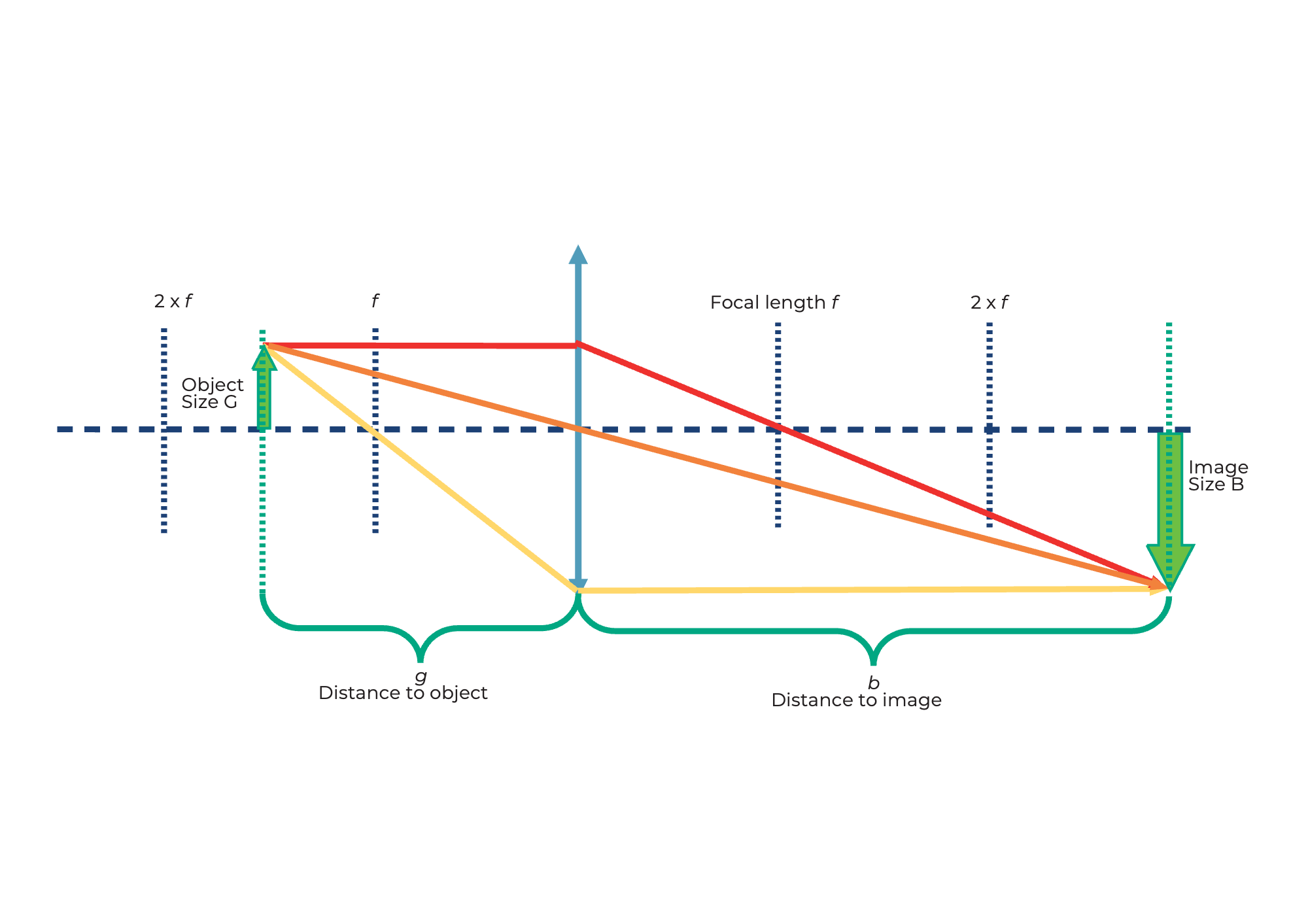
When an object is imaged through a converging lens, the position and size of the image depend on the distance (g) of the object to the lens and its focal length (f). The lens equation describes the relationship between image distance (b) and object distance (g):

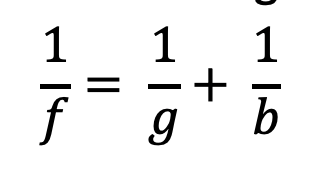
How big is the picture?

The magnification of the object on the screen can easily be calculated using the following formula:

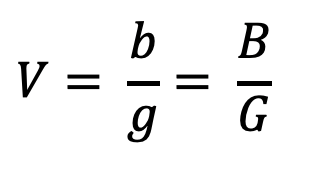
How the projector works

Check if your observation agrees with the calculation

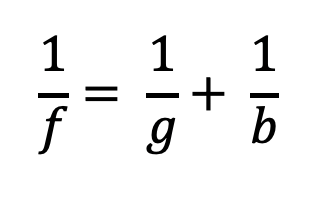
Calculate the magnification of the projector for the different values of g and b.

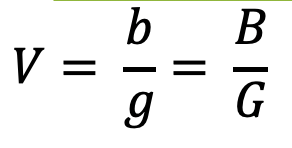
Our lens has a focal length of f= 40 mm.

For g = 50mm → b = 200mm

For g = 60 mm → b = 120 mm\

For g = 65 mm → b = 104 mm\

The projector always produces an enlarged, inverted (reversed) image. The position of the image and its magnification depend on the position and size of the object.

Tutorial: Determining the Focal Distance of a Positive Lens

Materials needed:

• Light source (e.g., room's illumiation)
• Positive lens
• Screen (e.g. table, piece of paper, etc.)

Instructions:

1. Position the positive lens so that it faces the light source. Align a screen parallel to the focal plane of the lens.
2. Modify the distance between the lens and the screen.
3. Carefully observe and record the position at which the light source forms a clear image on the surface of the screen.