lente
Lentes
En la óptica de rayos, la luz se representa como un conjunto de rayos (flechas), lo que simplifica las propiedades físicas de la luz. Un rayo tiene una dirección y, por lo tanto, se dibuja con una flecha. Una lente "refracta" el rayo, cambiando su dirección.
La distancia focal de una lente corresponde a la distancia desde la lente hasta el plano focal en el que se encuentra el punto focal. Se indica en milímetros (f = mm).
Lentes convergentes (positivas) y divergentes (negativas)
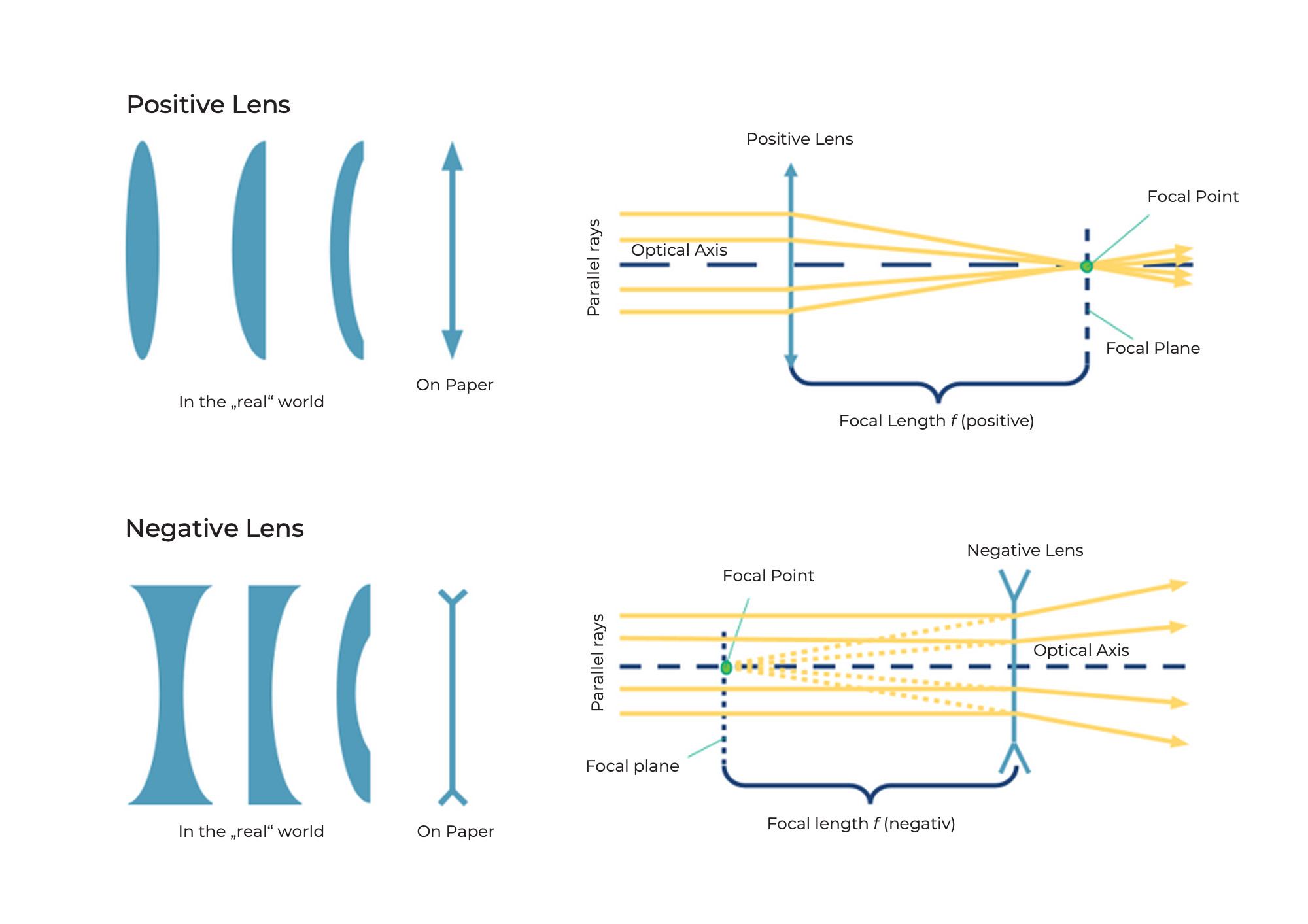
Las lentes convergentes refractan los rayos de luz que viajan paralelos al eje óptico en un punto llamado punto focal.
Las lentes divergentes refractan los rayos de luz que viajan paralelos al eje óptico como si provinieran de un punto llamado foco "virtual".
Las lentes “refractan” los rayos de luz
Puedes encontrar la distancia focal de la lente como un número impreso en el soporte de la lente. La MiniBOX incluye una lente convergente de 100 mm, dos lentes convergentes de 40 mm y una lente negativa de -50 mm. Los números indican la distancia focal.
La lente convergente también se llama lente positiva o convexa. La parte central de la lente es siempre más gruesa que los bordes.
La lente negativa (lente divergente) a veces también se llama lente negativa o cóncava. La parte central de la lente es siempre más delgada que los bordes.
Suponemos que nuestras lentes son las llamadas "lentes delgadas". Esto significa que podemos considerarlas como un plano único y no preocuparnos por su grosor. Esto hace que las explicaciones y cálculos sean mucho más fáciles.
Imagen con una lente
Ahora toma los cubos de lente. Con la lente adecuada, intenta descifrar la información de distancia focal en los cubos mostrados. Mueve la lente sobre la escritura hasta que sea del mismo tamaño que el texto "UC2".
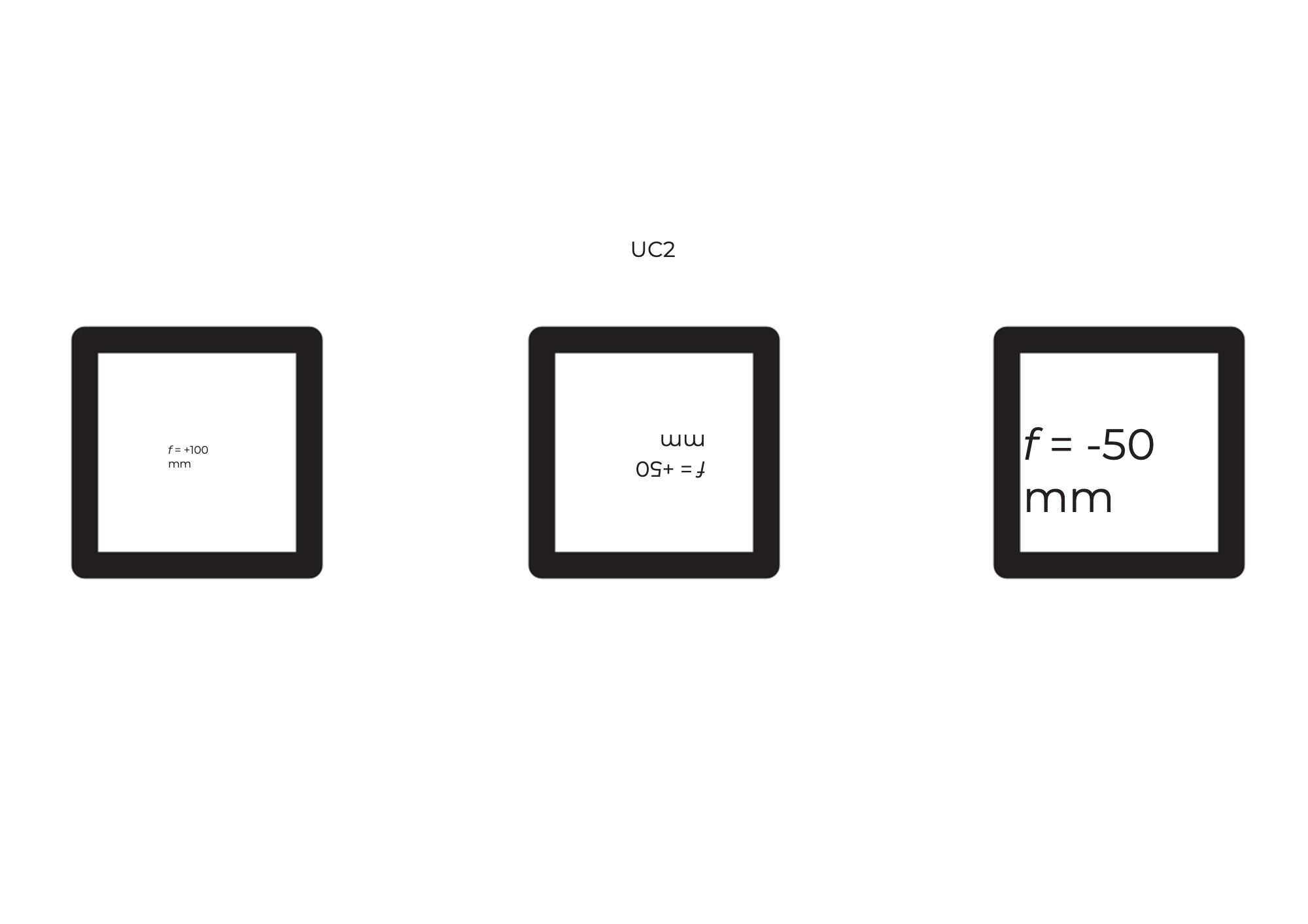
Imagen de un objeto a través de una lente positiva
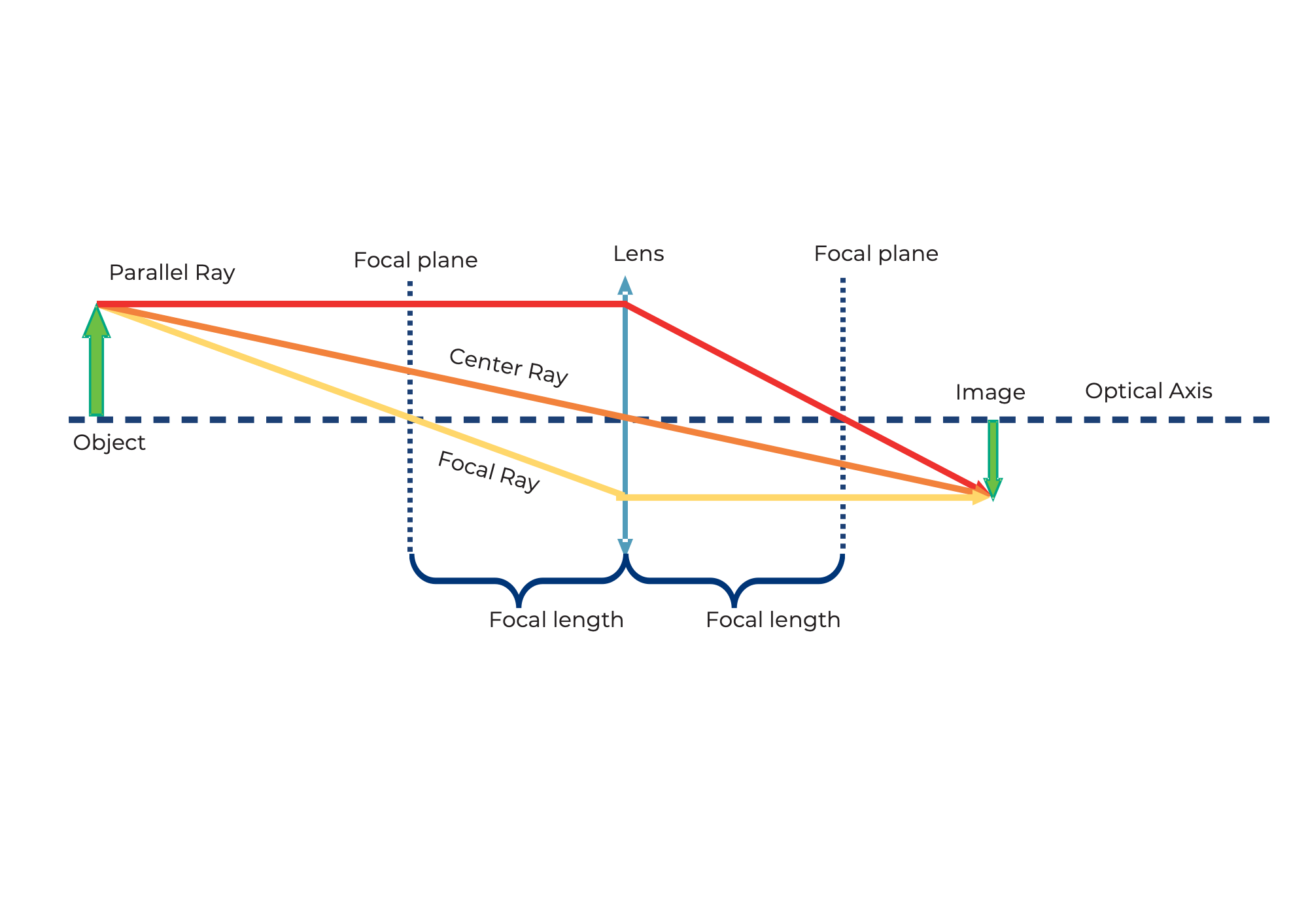
Tomemos la lente convergente como ejemplo. Comenzamos con un objeto (flecha verde) y observamos qué sucede con los rayos que parten de la parte superior. Hay infinitos rayos en todas las direcciones, pero para el dibujo, bastan los siguientes tres:
- El rayo central (naranja) pasa sin desviarse por el centro de la lente.
- El rayo focal (amarillo) también comienza en la punta de la flecha, pero pasa por el foco del lado del objeto a una distancia focal f. Después de la lente, continúa a la misma altura, pero ahora paralelo al eje óptico.
- El rayo paralelo (rojo) inicialmente corre paralelo al eje óptico, pero luego se refracta en la lente de modo que pasa por el punto focal del lado de la imagen a la distancia f.
La imagen se forma donde todos los rayos se cruzan. Este principio se aplica para todos los puntos o rayos que emanan de un objeto. Dependiendo de qué lente se use y de la posición del objeto, las propiedades de la imagen cambian, como tamaño, orientación y posición.
Imagen de un objeto a través de una lente negativa
En el caso de la lente negativa, usamos el mismo método para representar la trayectoria de los rayos. A diferencia del caso de la lente convergente, la imagen siempre está reducida y es virtual. La magnificación depende de la posición del objeto frente a la lente. A diferencia de la lente convergente, la imagen se crea en el lado del objeto y por lo tanto se llama imagen virtual. Puedes verla directamente con tus ojos, pero no proyectarla sobre una pantalla.
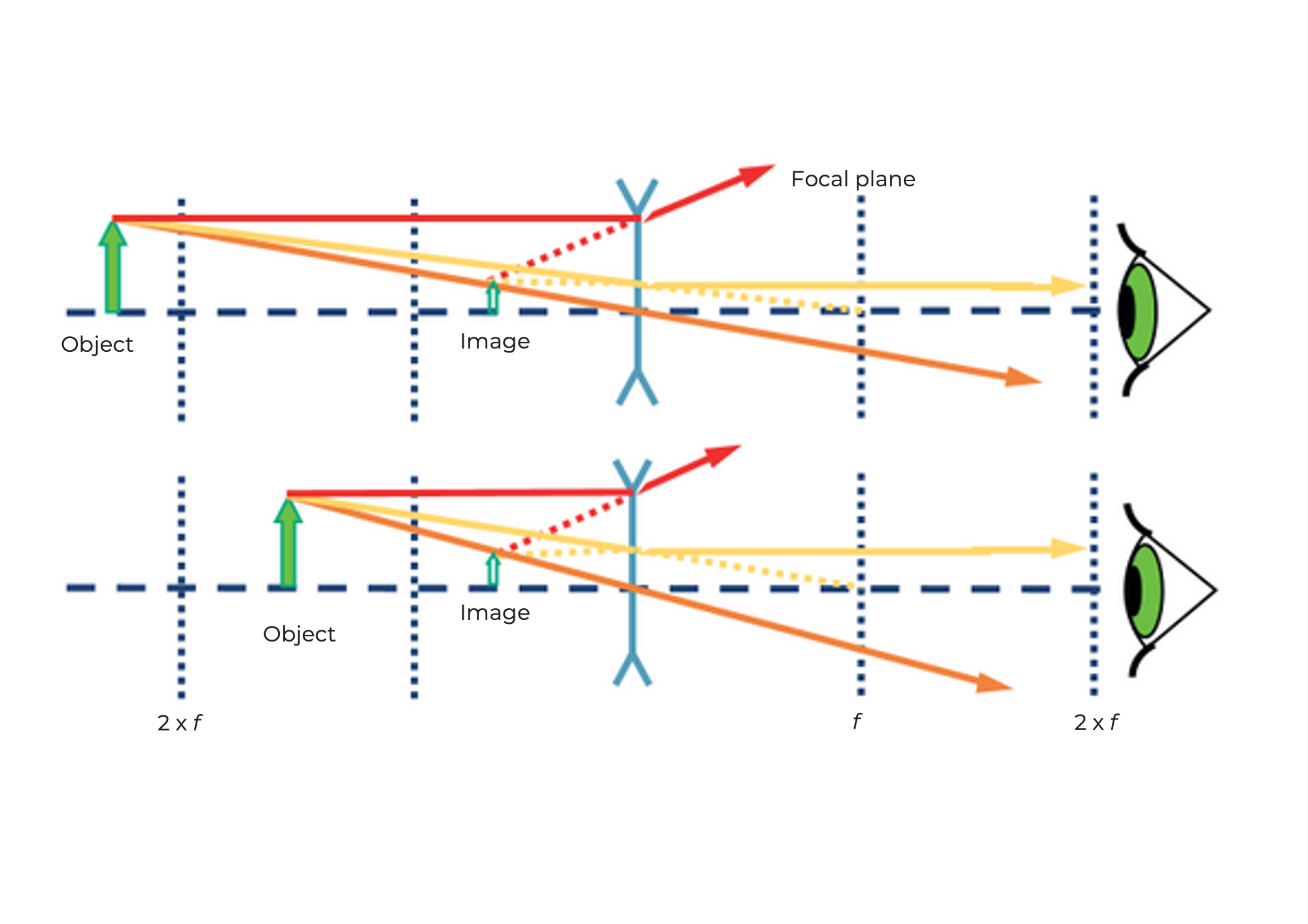
La lente convergente como lupa
Toma el cubo de lente UC2 con distancia focal f = 40 mm y úsalo como lupa.

Una lente en acción se puede ver aquí:
Esto es lo que hacen las lentes convergentes
Con las lentes convergentes, la imagen y la magnificación dependen de la posición del objeto.
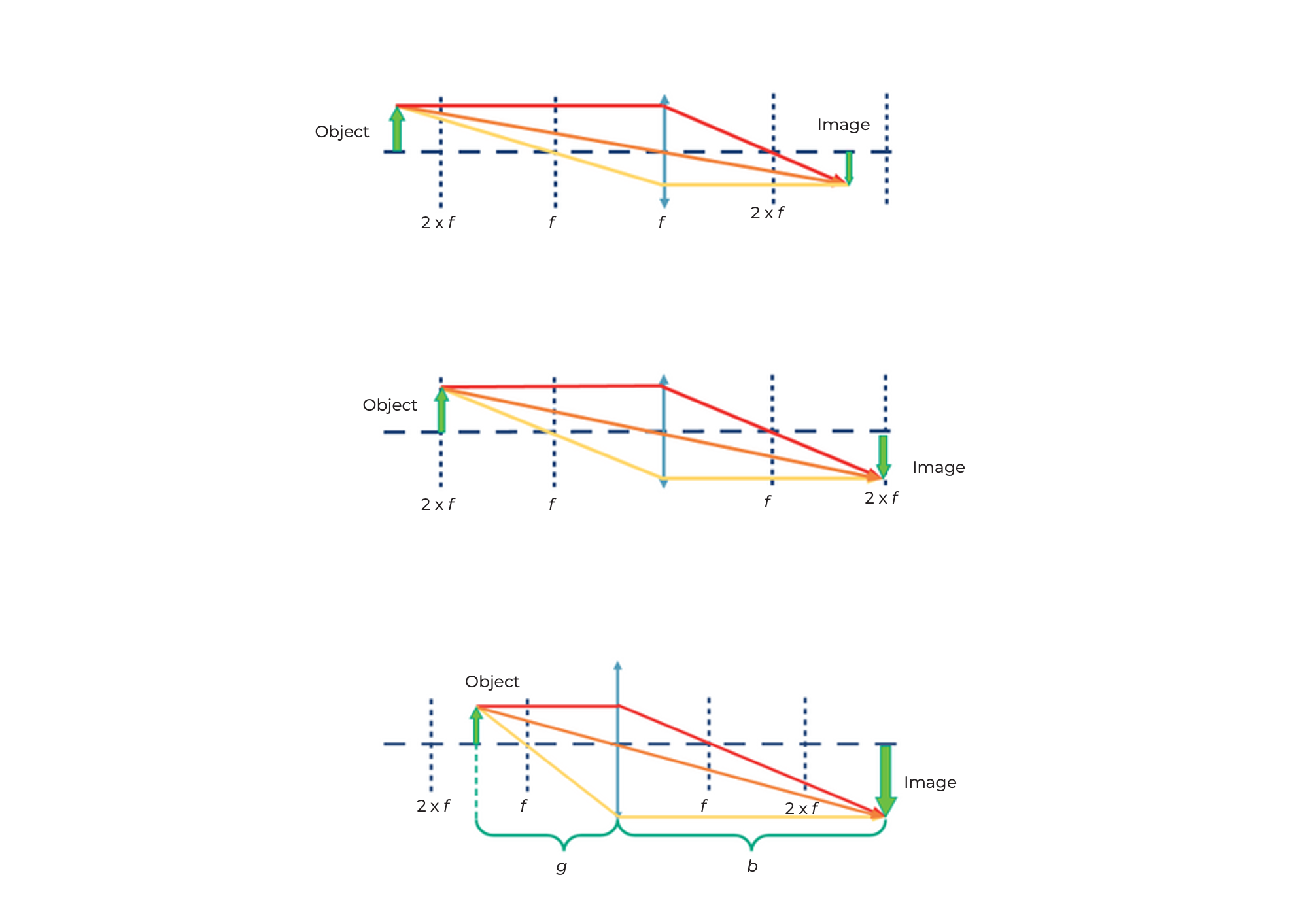
Si la distancia entre el objeto y la lente es más del doble de la distancia focal de la lente, entonces la imagen es...
- Invertida
- Invertida lateralmente
- Reducida
- Real
Si la distancia entre el objeto y la lente es exactamente el doble de la distancia focal, entonces la imagen es...
- Invertida
- Invertida lateralmente
- Del mismo tamaño
- Real
Si la distancia entre el objeto y la lente es mayor que la distancia focal y menor que el doble de la distancia focal, entonces la imagen es...
- Invertida
- Invertida lateralmente
- Ampliada
- Real
Distancia del objeto (g)
La distancia entre el objeto y el plano de la lente se llama g.
Distancia de la imagen (b)
La distancia entre el plano de la lente y la imagen formada por la lente se denomina b.
La lente convergente puede producir una imagen real. La imagen real puede verse en una pantalla.
Por eso la lupa amplía
¡Efecto lupa!
Si la distancia entre el objeto y la lente es menor que la distancia focal de la lente, entonces la imagen es...
- Derecha
- Correctamente orientada
- Ampliada
- Virtual
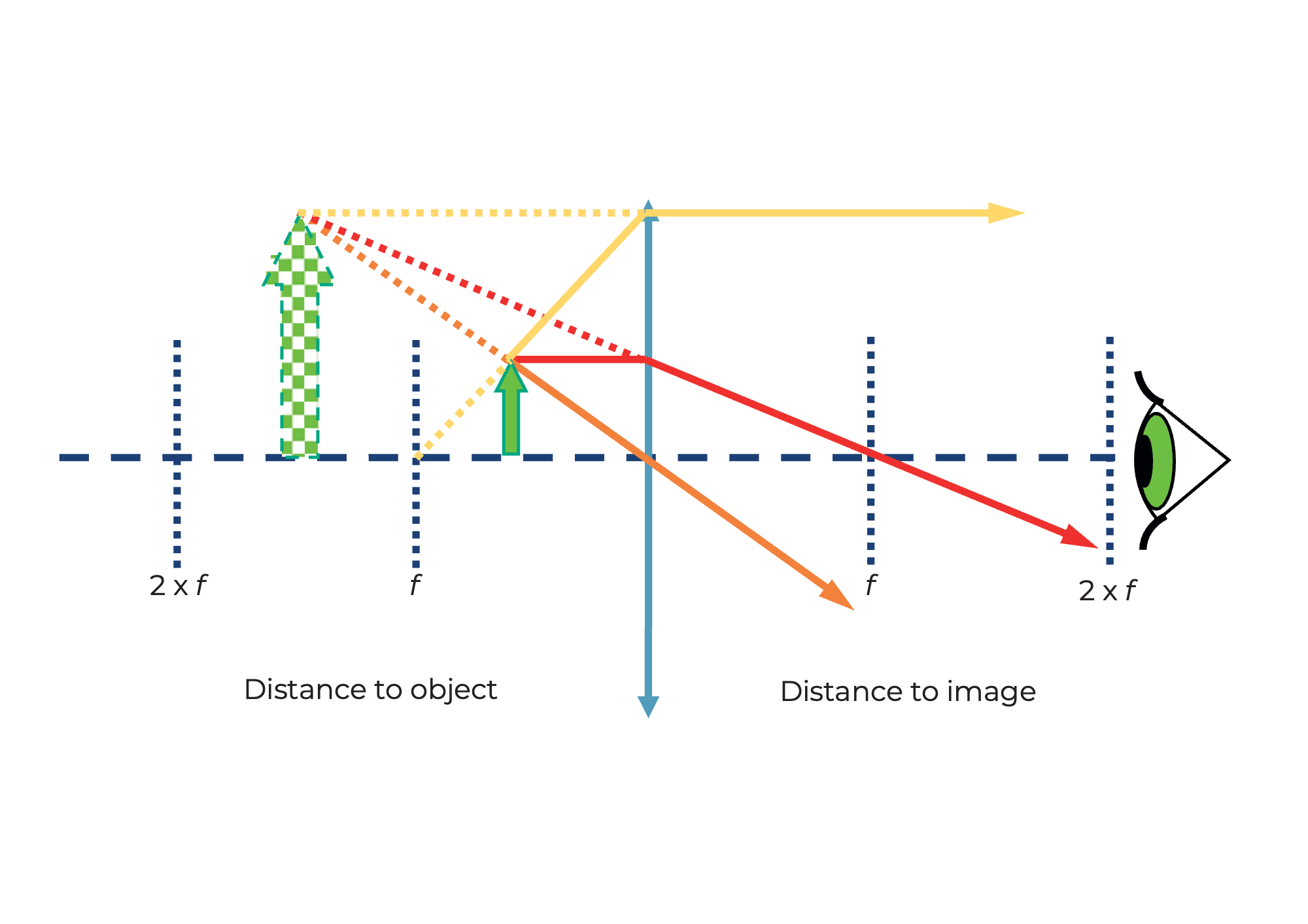
Calcula la magnificación de la lupa usando la siguiente fórmula:

250 mm es la distancia de visión clara – es decir, la distancia entre el objeto y el ojo a la que la mayoría de las personas pueden leer bien. Más sobre esto en la sección de “acomodación” del ojo.
¿Cómo funciona un proyector de cine?
Toma el cubo de lente UC2 con distancia focal f = 40 mm y colócalo detrás del cubo portamuestras. La distancia entre el objeto y la lente (es decir, la distancia del objeto g) debe ser de aproximadamente 50 mm. Si ahora iluminas el objeto con la linterna, lo verás enfocado a una distancia de aprox. 200 mm en la pared. Un proyector de cine tiene una tira de película en lugar del objeto y, por supuesto, una fuente de luz mucho más potente.
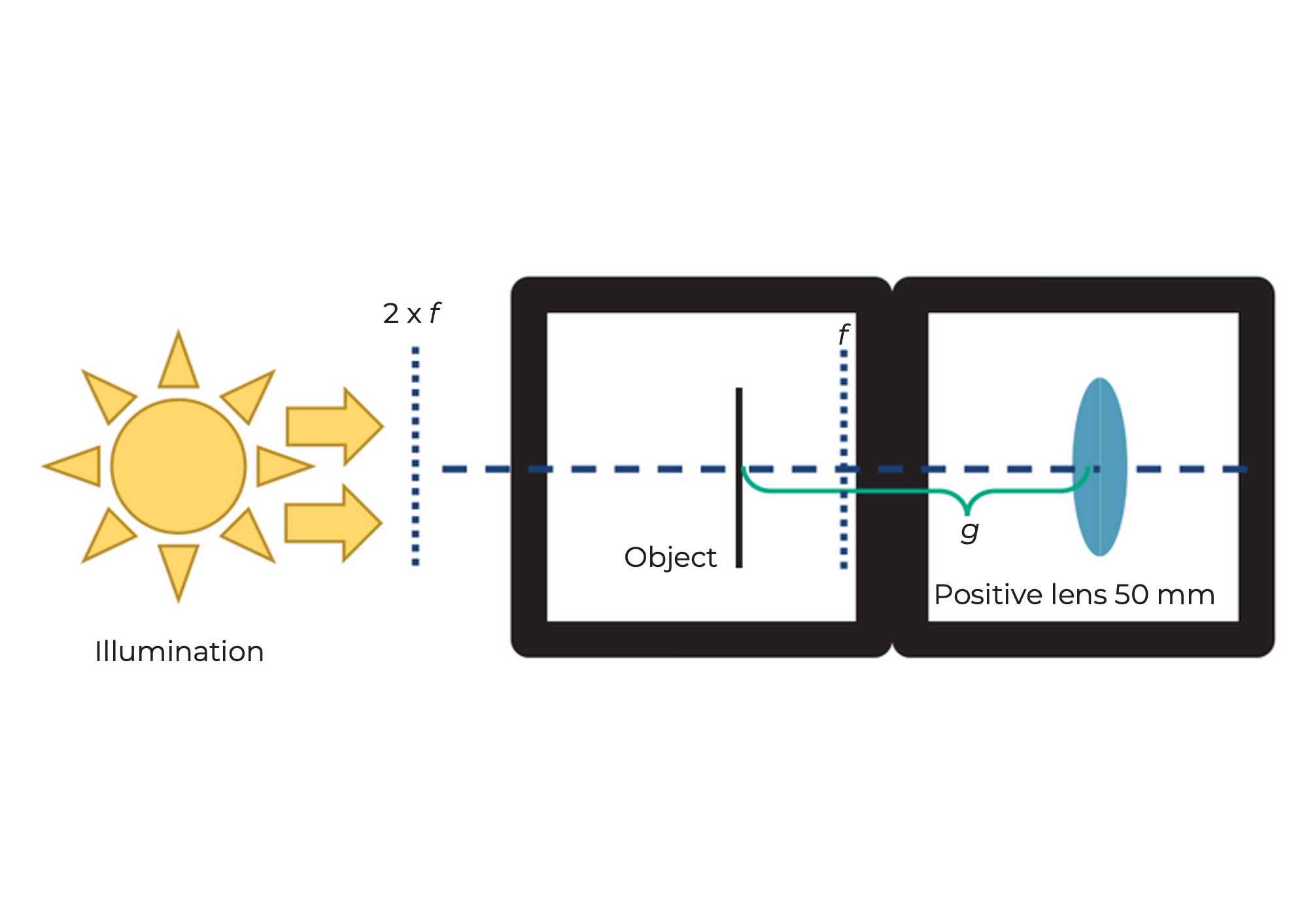
¿Cómo funciona un proyector de cine?
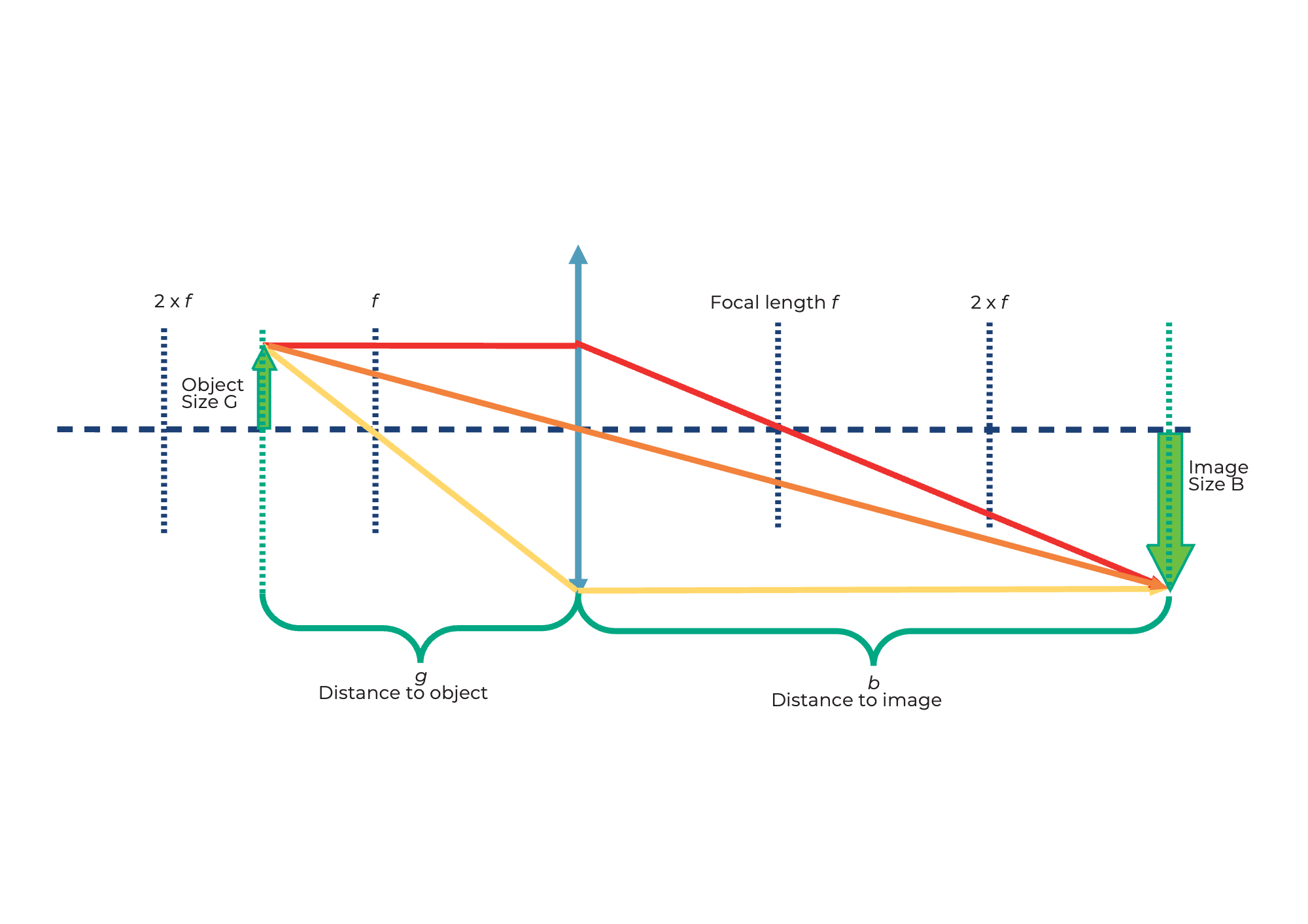
¿Dónde está la imagen?
Cuando un objeto se representa a través de una lente convergente, la posición y el tamaño de la imagen dependen de la distancia (g) del objeto a la lente y de su distancia focal (f).
La ecuación de la lente describe la relación entre la distancia de la imagen (b) y la distancia del objeto (g):
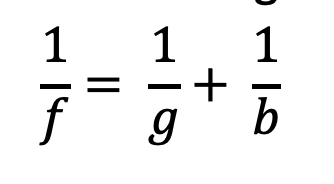
¿Qué tamaño tiene la imagen?
La ampliación del objeto en la pantalla se puede calcular fácilmente con la siguiente fórmula:
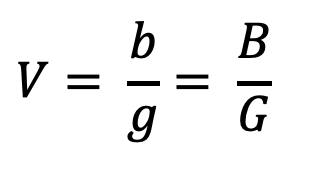
Cómo funciona el proyector
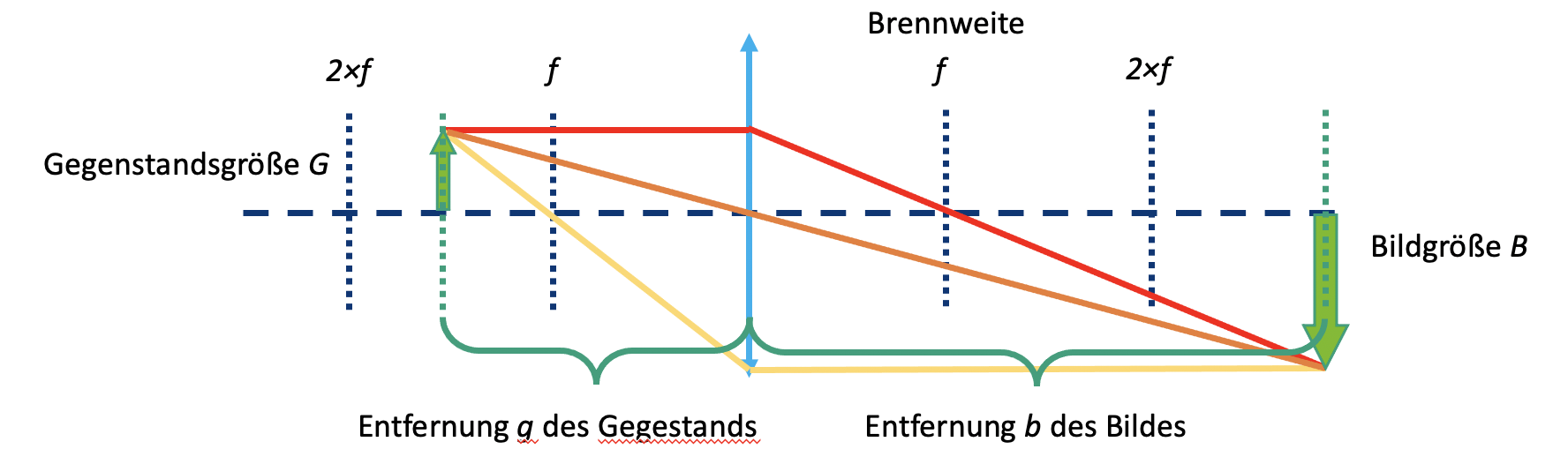
Verifica si tu observación concuerda con el cálculo
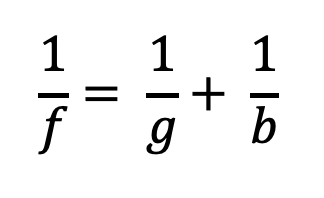
Calcula la ampliación del proyector para los diferentes valores de g y b.
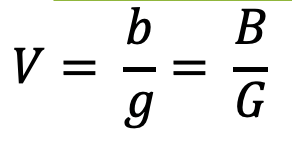
Nuestra lente tiene una distancia focal de f = 40 mm.
Para g = 50 mm → b = 200 mm
Para g = 60 mm → b = 120 mm
Para g = 65 mm → b = 104 mm
Tutorial: Determinar la distancia focal de una lente positiva
Materiales necesarios:
- Fuente de luz (por ejemplo, la iluminación de la sala)
- Lente positiva
- Pantalla (por ejemplo, una mesa, una hoja de papel, etc.)
Instrucciones:
- Coloca la lente positiva de modo que mire hacia la fuente de luz. Alinea una pantalla paralela al plano focal de la lente.
- Modifica la distancia entre la lente y la pantalla.
- Observa cuidadosamente y anota la posición en la que la fuente de luz forma una imagen nítida en la superficie de la pantalla.
